Informatik W09

Levin Ceglie

---

Outline

• Nachbesprechung Serie
• Rekursion I
• struct
• (Rekursion II)

Nachbesprechung Serie

• Erklärung const-correctness
• Aussagekräftige Funktionsnamen

Rekurion I

Aufgabe (Power Set)

Demonstration Set Klasse: In main.cpp Funktion set_demonstration() durchgehen.

5 Minuten Gedanken machen, nicht Programmieren!

Lösung gemeinsam an der Wandtafel erarbeiten:
Frage: Was ist die Potenzmenge von $\varnothing$?
Antwort: $\mathcal{P}(\varnothing )=\left\{\varnothing \right\}$.

Frage: Was ist die Potenzmenge von $\left\{a\right\}$?
Antwort: $\mathcal{P}(\left\{a\right\})=\left\{\varnothing ,\left\{a\right\}\right\}=\left\{\varnothing \right\}\cup \left\{\left\{a\right\}\right\}$.

Bemerke: $\mathcal{P}(\varnothing )\subseteq \mathcal{P}(\left\{a\right\})$, bzw. generell für Mengen $A\subseteq B$ gilt $\mathcal{P}(A)\subseteq \mathcal{P}(B)$.

Frage: Was is die Potenzmenge von $\left\{a,b\right\}$?
Antwort: $\mathcal{P}(\left\{a,b\right\})=\left\{\varnothing ,\left\{a\right\},\left\{b\right\},\left\{a,b\right\}\right\}=\left\{\varnothing ,\left\{a\right\}\right\}\cup \left\{\left\{b\right\},\left\{a,b\right\}\right\}$.

Frage: Was ist das Muster? Wie kommt man von $\mathcal{P}(\varnothing )⇝\mathcal{P}(\left\{a\right\})$ oder $\mathcal{P}(\left\{a\right\})⇝\mathcal{P}(\left\{a,b\right\})$?
Antwort: Wir bemerken, dass wenn immer ein neues Element dazu kommt, sind die schon gegebenen Teilmengen wieder Teilmengen und um die Restlichen zu erhalten muss man bei allen die man schon hatte das neue Element hinzufügen. Also zum Beispiel gilt

$$\begin{array}{rl}\mathcal{P}(\left\{a,b,c\right\})& =\left\{\varnothing ,\left\{a\right\},\left\{b\right\},\left\{c\right\},\left\{a,b\right\},\left\{a,c\right\},\left\{b,c\right\},\left\{a,b,c\right\}\right\}\\ & =\left\{\varnothing ,\left\{a\right\},\left\{b\right\},\left\{a,b\right\}\right\}\cup \left\{\left\{c\right\},\left\{a,c\right\},\left\{b,c\right\},\left\{a,b,c\right\}\right\}\\ & =\left\{\varnothing ,\left\{a\right\},\left\{b\right\},\left\{a,b\right\}\right\}\cup \left\{Y\cup \left\{c\right\}\mid Y\in \left\{\varnothing ,\left\{a\right\},\left\{b\right\},\left\{a,b\right\}\right\}\right\}\\ & =\mathcal{P}(\left\{a,b\right\})\cup \left\{Y\cup \left\{c\right\}\mid Y\in \mathcal{P}(\left\{a,b\right\})\right\}\end{array}$$

Frage: Mit dem Wisse, wie könnte ein Rekursiver Algorithmus zur Berechnung der Potenzmenge einer beliebigen Menge $S$ aussehen?
Antwort:

1. Wähle beliebiges $x\in S$, wobei $\left|S\right|=n$
2. Setze $S^{\prime }:=S\setminus \left\{x\right\}$
3. Berechne $\mathcal{P}(S^{\prime })$, wobei $\left|S\right|=n-1$
4. Nun gilt $\mathcal{P}(S)=\mathcal{P}(S^{\prime })\cup \left\{Y\cup \left\{x\right\}\mid Y\in \mathcal{P}(S^{\prime })\right\}$

Frage: Was fehlt im obigen Algorithmus, damit er funktioniert?
Antwort: Base Case! Wir setzen $\mathcal{P}(\varnothing )=\left\{\varnothing \right\}$.

Pair Programming für 10 Minuten

Gemeinsame Implementation
Lösung:

#include "solution.h"
 
SetOfCharSets power_set(const CharSet& set) {
  // base case: empty set
  if (set.size() == 0) {
    return SetOfCharSets(CharSet());
  }
 
  // set has at least 1 element
  // split set into two sets.
  // (1) a set containing only the first element
  // (2) a set containing all elements except the first element
  CharSet first_element_subset = CharSet(set.at(0));
  CharSet remaining_subset = set - first_element_subset;
 
  // get power set for remaining subset
  SetOfCharSets remaining_subset_power_set = power_set(remaining_subset);
 
  // init result with power set of remaining subset
  SetOfCharSets result = remaining_subset_power_set;
 
  // add first element to every set in the powerset
  auto n = remaining_subset_power_set.size();
  for (unsigned int i = 0; i < n; ++i) {
    result.insert(first_element_subset + remaining_subset_power_set.at(i));
  }
 
  return result;
}

Structs

In einer struct kann man beliebige bereits definierte Datentypen kombinieren zu einem neuen “Datentypen”. Zum Beispiel, wenn man die komplexen Zahlen implementieren möchte, könnte ich

struct complex_number{
	double x;
	double y;
};

und dann könnte man die Multiplikation von komplexen Zahlen durch Überladung des * Operators wie folgt implementieren.

complex_number operator*(const complex_number& a, const complex_number& b){
  return complex_number{a.x*b.x - a.y*b.y, a.x*b.y + a.y*b.x};
}

und initialisieren einer einer struct geschieht per Default wie folgt

complex_number a = {1, 2}; // x==1, y==2

Aufgabe (Geometry Exercise)

Pair Programming ~20 Minuten

Gemeinsame Implementation:
Lösung:

#include <iostream>
 
// Datastructure representing a 3D vector
struct vec {
  double x;
  double y;
  double z;
};
 
// helper function to print a vector
void print_vec(const vec& v) {
  std::cout << "(" << v.x << "," << v.y << "," << v.z << ")";
}
 
 
// Subtask 1: adding vectors----------------------------
// POST: returns the sum of a and b
vec sum(const vec& a, const vec& b) {
  // version 1: compact, used for the rest of the example
  return {a.x + b.x, a.y + b.y, a.z + b.z};
  
  // version 2: longer but maybe easier to understand
  // vec tmp;
  // tmp.x = a.x + b.x;
  // tmp.y = a.y + b.y;
  // tmp.z = a.z + b.z;
  // return tmp;
}
//------------------------------------------------------
 
 
 
// Subtask 2: defining a line in 3D---------------------
struct line {
  vec start;
  vec end;  // INV: start != end
};
 
// helper function to print a vector
void print_line(const line& l) {
  print_vec(l.start);
  std::cout << " <-> ";
  print_vec(l.end);
}
//------------------------------------------------------
 
 
 
// Subtask 3: shifting line by a vector-----------------
// POST: returns a new line obtained by shifting l
// by v.
line shift_line(const line& l, const vec& v) {
  return {sum(l.start, v), sum(l.end, v)};
}
//------------------------------------------------------
 
 
 
// Subtask 4: overloading the + operator for vectors----
vec operator+(const vec& a, const vec& b) { return sum(a, b); }
//------------------------------------------------------
 
 
 
// Subtask 5: overloading the + operator for lines
 
// version 1: use the shift_line function
line operator+(const line& l, const vec& v) { return shift_line(l, v); }
 
// version 2: make use of the overloaded + operator for vectors
// line operator+(const line& l, const vec& v) { return {l.start + v, l.end + v}; }
 
//------------------------------------------------------
 
 
 
// Optional Subtask 6: overloading the << operators-----
std::ostream& operator<<(std::ostream& os, const vec& v) {
  os << "(" << v.x << "," << v.y << "," << v.z << ")";
  return os;
}
std::ostream& operator<<(std::ostream& os, const line& l) {
  os << l.start << " <-> " << l.end;
  return os;
}
//------------------------------------------------------
 
 
 
int main() {
	...
}

Rekursion II

Aufgabe (Towers of Hanoi)

Bemerkung: Dies ist eine eher schwierige Aufgabe.

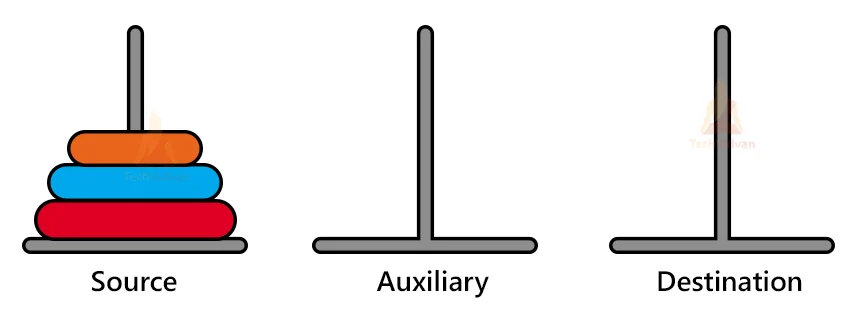
Das Spiel besteht aus drei gleich großen Stäben, auf die mehrere gelochte Scheiben gesteckt werden, alle verschieden groß. Zu Beginn liegen alle Scheiben auf dem linken Stab, der Größe nach geordnet, mit der größten Scheibe unten und der kleinsten oben (siehe Bild). Ziel des Spiels ist es, den kompletten Scheiben-Stapel vom linken Stab auf den rechten Stab zu versetzen. Hierbei gelten zwei Regeln:

1. Es darf immer nur eine Scheibe gleichzeitig bewegt werden.
2. Die bewegte Scheibe darf nicht auf eine kleinere Scheibe gesteckt werden.

Folglich sind zu jedem Zeitpunkt des Spieles die Scheiben auf jedem Feld der Größe nach geordnet
- Türme von Hanoi – Wikipedia

Hinweis: Was ist der Base Case?
Hinweis: Betrachte den Fall mit zwei Scheiben und verallgemeineren diese zu $n$ Scheiben mittels Rekursion.

Lösung:

#include <iostream>
#include <string>
 
// POST: Prints instructions how to transfer n discts from src to dst.
void move(int n, const std::string& src, const std::string& aux, const std::string& dst) {
  if (n == 1) {
    // base case ('move' the disc)
    std::cout << src << " --> " << dst << std::endl;
  } else {
    // recursive case
    move(n-1, src, dst, aux);
    move(1, src, aux, dst );
    move(n-1, aux, src, dst);
  }
}
 
int main() {
  int n;
  std::cin >> n;
  move(n, "left" , "middle", "right" );
  return 0;
}