Informatik W08

Levin Ceglie

---

Outline

• Quiz
• Nachbesprechung Serie
• Multidimensionale Vektoren
• Rekursion

Nachbesprechung Serie

• Beachte, dass

bool foo(){
	if(exp){
		return true;
	}else{
		return false;
	}
}

ist äquivalent zu

bool foo(){
	return exp;
}

• Verwende assert für Überprüfung der PRE-condition.
• #pragma once
• Achtet bei PRE conditions auf Edge-cases!

bool f3(unsigned int n) {
  unsigned int i = 2;
  for (; n % i != 0; ++i);
  return n == i;
}

Was passiert bei n==0 oder n==1?

• Die Typen von Funktionsargumenten gehören nicht in die PRE condition. Diese sind von der Funktion vorgegeben.

Multidimensionale Vektoren

Aufgabe (Matrix Transpose)

Es sind zwei Varianten zur Initialisierung einer Matrix gegeben:

imatrix read_matrix() {
  unsigned int r, c;
  std::cin >> r >> c;
  imatrix matrix = imatrix(0); // construct a matrix with zero rows
  for (unsigned int row_index = 0; row_index < r; row_index++) {
    irow row = irow(0); // construct a row with zero entries
    for (unsigned int col_index = 0; col_index < c; col_index++) {
      int element;
      std::cin >> element;
      row.push_back(element);
    }
    matrix.push_back(row);
  }
  return matrix;
}

und

imatrix read_matrix() {
  unsigned int r, c;
  std::cin >> r >> c;
  imatrix matrix(r, irow(c, 0)); // construct a r x c matrix filled with zeros
  for (unsigned int row_index = 0; row_index < r; row_index++) {
      for (unsigned int col_index = 0; col_index < c; col_index++) {
          int element;
          std::cin >> element;
          matrix.at(row_index).at(col_index) = element;
      }
  }
  return matrix;
}

Bemerke, dass die zweite alle Einträge der Matrix auf einmal initialisiert. In der ersten Version geschieht dies Zeile für Zeile. Wir verwenden die zweite Version, da dort die Matrixstruktur besser zur Geltung kommt.

Lösung:

#include <iostream>
#include <vector>
#include <cassert>
 
using irow = std::vector<int>;
using imatrix = std::vector<irow>;
 
// POST: Returns the number of rows.
unsigned int get_rows(const imatrix& matrix) {
  return matrix.size();
}
 
// POST: Returns the number of columns.
unsigned int get_cols(const imatrix& matrix) {
  if (get_rows(matrix) > 0) {
    return matrix.at(0).size();
  }
  // Empty matrix has no columns.
  return 0;
}
 
 
// // POST: Returns a matrix that was read from the standard input.
imatrix read_matrix() {
  unsigned int r, c;
  std::cin >> r >> c;
  imatrix matrix(r, irow(c, 0)); // construct a r x c matrix
                                 // filled with zeros
  for (unsigned int row_index = 0; row_index < r; row_index++) {
      for (unsigned int col_index = 0; col_index < c; col_index++) {
          int element;
          std::cin >> element;
          matrix.at(row_index).at(col_index) = element;
      }
  }
  return matrix;
}
 
// POST: Writes the matrix into standard output.
void write_matrix(const imatrix& matrix) {
  unsigned int r, c;
  r = get_rows(matrix);
  c = get_cols(matrix);
  std::cout << r << " " << c << std::endl;
  for (unsigned int row_index = 0; row_index < r; row_index++) {
    for (unsigned int col_index = 0; col_index < c; col_index++) {
      std::cout << matrix.at(row_index).at(col_index) << " ";
    }
    std::cout << std::endl;
  }
}
 
// POST: Return a matrix that is a transpose of the input matrix.
imatrix transpose_matrix(const imatrix& matrix) {
  unsigned int r, c;
  r = get_rows(matrix);
  c = get_cols(matrix);
  imatrix transposed_matrix(c, irow(r, 0)); // construct a c x r matrix 
                                            // filled with zeros
  for (unsigned int row_index = 0; row_index < r; row_index++) {
    for (unsigned int col_index = 0; col_index < c; col_index++) {
      transposed_matrix.at(col_index).at(row_index) =
          matrix.at(row_index).at(col_index);
    }
  }
  return transposed_matrix;
}
 
int main () {
  imatrix matrix = read_matrix();
  imatrix transposed_matrix = transpose_matrix(matrix);
  write_matrix(transposed_matrix);
  return 0;
}

Rekursion

Aufgabe (Partial Sums)

Hinweis: Base Case!

Lösung:

#include<iostream>
 
unsigned int partial_sum(const unsigned int n) {
  if (n == 0)
    return 0;
  else {
    // print descending
    // std::cout << n << std::endl;
    unsigned int partial = partial_sum(n - 1);
    // print ascending
    std::cout << n << std::endl;
    return n + partial;
  }
}
 
int main() {
  std::cout << "n = ";
  unsigned int n;
  std::cin >> n;
  std::cout << partial_sum(n) << std::endl;
  return 0;
}
 

Aufgabe (Power Function)

Lösung:

#include <iostream>
 
// POST: result == x^n
unsigned int power (const unsigned int x, const unsigned int n) {
  if (n == 0) {
    return 1;
  } else if (n == 1) {
    return x;
  }
  
  unsigned int rem = n%2 ? x : 1;
  unsigned int tmp = power(x,n/2);
  return tmp*tmp*rem;
}
 
int main() {
  int x;
  unsigned int n;
  
  std::cin >> x >> n;
  
  unsigned int p = power(x, n);
  
  std::cout << p << std::endl;
  
  return 0;
}

Rekursionsanalyse:
Wir wollen die Rekursionstiefe in Abhängigkeit von $n$ bestimmen. Sei $T(n)$ die Rekursionstiefe in Abhängigkeit von $n$. Wir bemerken, dass die folgende Rekursionsformel gilt

$$T(n)=\{\begin{array}{ll}1& n\in \left\{0,1\right\}\\ 1+T\left(\frac{n}{2}\right)& \text{sonst}\end{array}$$

Angenommen $n=2^k$ für ein $k\in \mathbb{N}$. Wir berechnen

$$T(2^k)=1+T(2^{k-1})=1+1+T(2^{k-2})=\cdots =i+T(2^{k-i})=k+1$$

Wir vermuten also $T(2^k)=k+1$ und wegen $n=2^k$ gilt $k={\log }_{2}n$ und somit erhalten wir die Vermutung

$$T(n)=1+{\log }_{2}n$$

für $n\ge 1$. Wir beweisen diese Vermutung nun noch mittels Induktion. Wir bemerken $T(1)=1+{\log }_{2}1=1$, womit die Vermutung für den Fall $n=1$ gilt. Nehmen wir nun an die Aussage gilt für alle $n^{\prime }<n$ für ein beliebiges $n\ge 1$. Wir folgern

$$\begin{array}{rl}T(n)& =1+T\left(\frac{n}{2}\right)\\ \text{I.A.}& =1+1+{\log }_2\left(\frac{n}{2}\right)\\ & =2+{\log }_{2}n-{\log }_{2}2\\ & =1+{\log }_{2}n\end{array}$$

Dies schliesst den Induktionsschritt, womit die Aussge für alle $n\ge 1$ folgt.

Aufgabe (Towers of Hanoi)

Bemerkung: Dies ist eine eher schwierige Aufgabe.

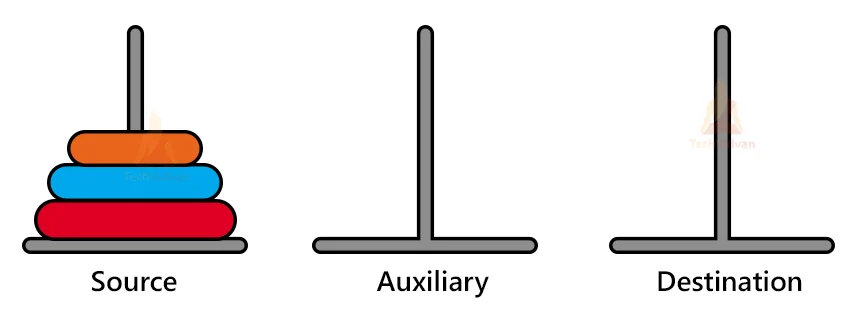
Das Spiel besteht aus drei gleich großen Stäben, auf die mehrere gelochte Scheiben gesteckt werden, alle verschieden groß. Zu Beginn liegen alle Scheiben auf dem linken Stab, der Größe nach geordnet, mit der größten Scheibe unten und der kleinsten oben (siehe Bild). Ziel des Spiels ist es, den kompletten Scheiben-Stapel vom linken Stab auf den rechten Stab zu versetzen. Hierbei gelten zwei Regeln:

1. Es darf immer nur eine Scheibe gleichzeitig bewegt werden.
2. Die bewegte Scheibe darf nicht auf eine kleinere Scheibe gesteckt werden.

Folglich sind zu jedem Zeitpunkt des Spieles die Scheiben auf jedem Feld der Größe nach geordnet
- Türme von Hanoi – Wikipedia

Hinweis: Was ist der Base Case?
Hinweis: Betrachte den Fall mit zwei Scheiben und verallgemeineren diese zu $n$ Scheiben mittels Rekursion.

Lösung:

#include <iostream>
#include <string>
 
// POST: Prints instructions how to transfer n discts from src to dst.
void move(int n, const std::string& src, const std::string& aux, const std::string& dst) {
  if (n == 1) {
    // base case ('move' the disc)
    std::cout << src << " --> " << dst << std::endl;
  } else {
    // recursive case
    move(n-1, src, dst, aux);
    move(1, src, aux, dst );
    move(n-1, aux, src, dst);
  }
}
 
int main() {
  int n;
  std::cin >> n;
  move(n, "left" , "middle", "right" );
  return 0;
}