Informatik W04

Levin Ceglie

Outline

• Repetition Vorlesung via Quiz
• Expressions
• Scopes
• Loops

Expressions

Ähnlich wie bei den Operatoren haben in C++ auch die verschiedenen Datentypen Präzedenzen, auf die man achten muss. Folgende Reihenfolge sollte man sich merken

$$\text{bool}<\text{char}<\text{int}<\text{unsigned int }<\text{ float}<\text{double}$$

Persöhnliche Empfehlung: Präzedenzen auf den Spick für die Prüfung!

Beispiele

Aufgabe (Auswertung von Expressions) (optional)

1. Bei welche der folgenden Zeichenfolgen handelt es sich nicht um C++ Expressions und wieso? Hier sind x und y Variablen vom Typ in
   (a) (y++ < 0 && y < 0) + 2.0
   (b) y = (x++ = 3)
   (c) 3.0 + 3 - 4 + 5
   (d) 5 % 4 * 3.0 + true * x++

2. Für alle gültigen C++ Expressions die du gefunden hast, entscheide ob es sich um L-Werte oder R-Werte handelt.

3. Finde den Wert der gültigen Expressions unter der Annahme, dass zu Beginn x== 1 und y== -1.

Lösung:
(a)

(y++ < 0 && y < 0) + 2.0
( -1 < 0 && y < 0) + 2.0 // Danach : y==0
( true && y < 0) + 2.0
( true && false ) + 2.0
( false ) + 2.0
0.0 + 2.0
2.0

R-Wert

(b)

y = (x++ = 3)

Ungültig, man versucht einem R-Wert (x++) einen Wert zuzuweisen.

(c)

3.0 + 3 - 4 + 5
((3.0 + 3) - 4) + 5
((3.0 + 3.0) - 4) + 5
(6.0 - 4) + 5
(6.0 - 4.0) + 5
2.0 + 5
2.0 + 5.0
7.0

R-Wert

(d)

5 % 4 * 3.0 + true * x++
((5 % 4) * 3.0) + ( true * ( x ++) )
(1 * 3.0) + ( true * ( x ++) )
(1.0 * 3.0) + ( true * ( x ++) )
3.0 + ( true * ( x ++) )
3.0 + ( true * 1)
3.0 + (1 * 1)
3.0 + 1
3.0 + 1.0
4.0

R-Wert

Scopes

Ein Scope (Gültigkeitsbereich) wird meistens (nicht immer!) mit {} gekennzeichnet . Wird eine Variable in einem Scope deklariert, so ist sie innerhalb des Scopes und auch in allen darin verschachtelten Scopes sichtbar. Am Ende des Scope wird der Speicherplatz wieder freigegeben und die Variable ist nicht mehr sichtbar .

Beispiel

#include <iostream>
 
int main() {
  int x = 1;
  
  for (int i = 1; i < 5; ++i) {
    x *= 2;
  }
  
  std::cout << x << std::endl; // Funktioniert, da x in diesem Scope definiert wurde
  std::cout << i << std::endl; // Fehler, da i nur im Scope der for-loop sichtbar war
 
  return 0;
}

In diesem Beispiel wird die Variable i im Scope der For-Loop initialisiert und wird deswegen am Ende des selben Scopes wieder gelöscht. Dies führt zu eine Fehler, wenn man nach der Ende der For-Loop versucht auf diese Variable i zuzugreifen.

Beispiel

#include <iostream>
 
int main() {
  int x = 2;
  int a = 5;
  
  {
    int x = 3;
    x = a*x;
    a = 2*x;
  }
  
  std::cout << x << std::endl; // gibt 2 aus
  std::cout << a << std::endl; // gibt 30 aus
 
  return 0;
}

Dieses Beispiel soll das sogennante “shadowing” von Variablen illustrieren (siehe Variable shadowing - Wikipedia). Hier wird in einem äusseren Scope eine Variable x definiert und anschliessend in einem inneren Scope eine neue Variable mit dem selben Namen initialisiert. Dies führt dazu, dass im inneren Scope das äussere x vom inneren x überdeckt (“shadowed”) wird. Alle operation die ein x im inneren Scope verwenden, verändern somit die äussere Variable x nicht. Am Ende des inneren Scopes werden dann alle Variablen die in diesem Scope definiert wurden, inklusive x, gelöscht und ab da übernimmt wieder das x des äusseren Scopes.

Siehe C++ Guide (auf der Vorlesungsseite verlinkt) für eine weitere nützliche Erklärung.
Siehe Scope - cppreference.com für eine sehr genaue und ausführliche Erklärung (geht evtl. über den Vorlesungsstoff hinaus).

Loops

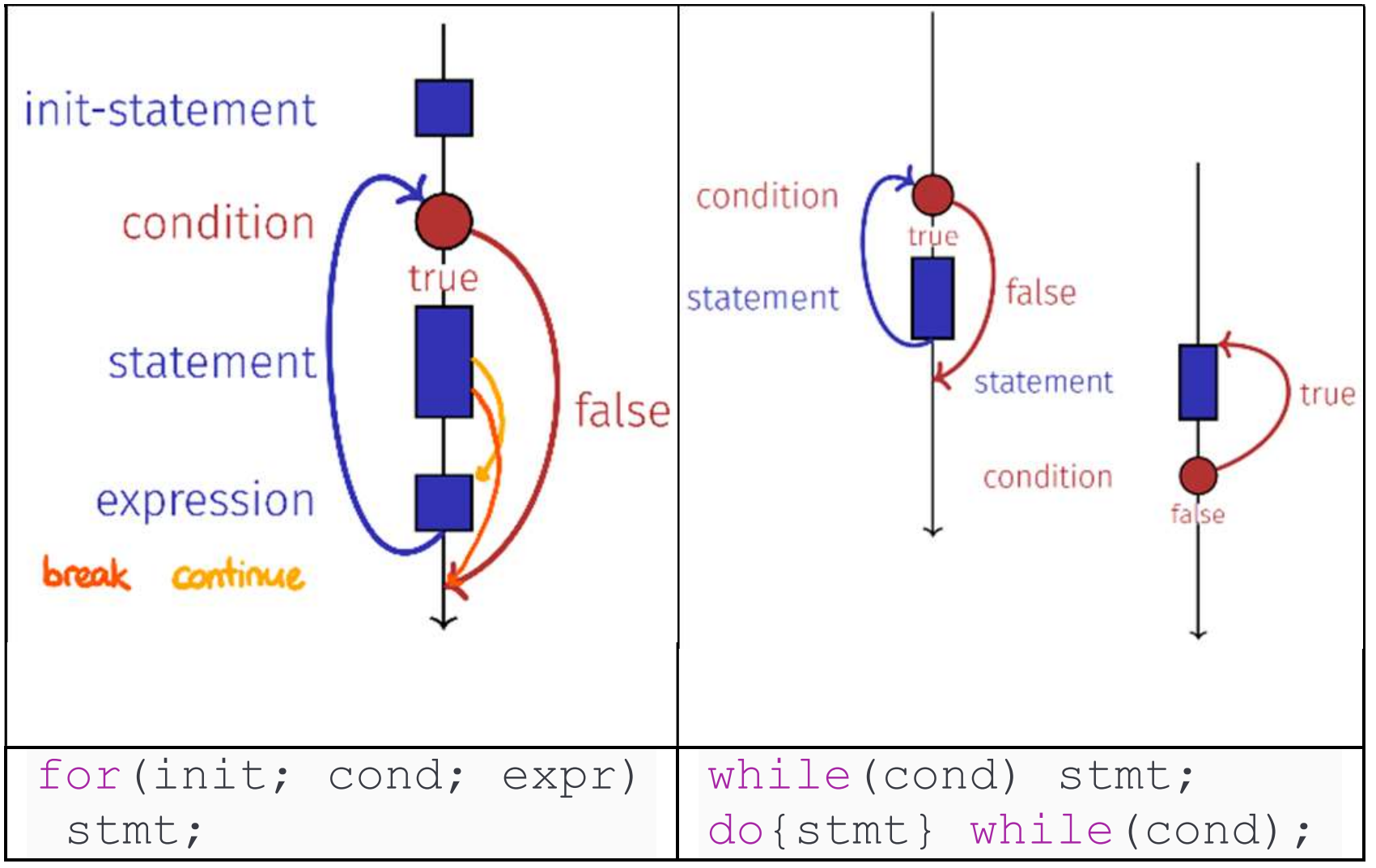
Aufgabe (Loop Correctness)

Betrachte folgende drei Schlaufen und finde heraus, ob und falls ja wie sie sich unterscheiden.

unsigned int n;
unsigned int i;
std::cin >> n;

Loop 1:

for (i = 1; i <= n; ++i) {
	std::cout << i << "\n";
}

Loop 2:

i = 0;
while (i < n) {
    std::cout << ++i << "\n";
}

Loop 3:

i = 1;
do {
	std::cout << i++ << "\n";
} while (i <= n);

Lösung:

• Anders wie in der Loops 1 und 2 gibt Loop 3 für den input n==0 eine 1 aus. Das liegt daran, dass der Ausdruck innerhalb einer “do-while” Schleife mindestens immer einmal ausgeführt wird.
• Falls n die grösst mögliche Zahl ist (für unsigne int), so sind Loops 1 und 3 endlosschleifen, weil die Bedingung i<=n stets erfüllt ist.

Aufgabe (Loop Conversion)

Konvertiere die folgende For-Loop in eine äquivalente While-Loop:

for (int i = 0; i < n; ++i){
	BODY
}

Konvertiere die folgende While-Loop in eine äquivalente For-Loop:

while (condition){
	BODY
}

Konvertiere die folgende Do-While-Loop in eine äquivalente For-Loop:

do{
	BODY
}while (condition);

Bemerkung: Es werden keine continue statements verwendet, denn in speziellen Fällen wurde dies die Umwandlung unmöglich machen.

Lösung:
In obiger Reihenfolge:

{ // Dieser zusätzliche Block wird verwendet um den Gültigkeitsbereich von i einzuschränken
	int i = 0;
	while (i < n) {
		BODY
		++i;
	}
}

for ( ;condition; ){
	BODY
}

BODY
for ( ;condition; )
	BODY

Aufgabe (Taylor Series)

Schreibe ein C++ Programm, das $\sin x$ mit einer Präzision von $0.000001$ berechnet. Verwende dafür die sogenannte Maclaurin series:

$$\sin x=\sum _{n=0}^{\infty }\frac{(-1{)}^n}{(2n+1)!}{x}^{2n+1}$$

Hinweis 1: Überlege dir wie du den $n$-ten Term berechnen kannst, wenn du den $(n-1)$-ten Term schon kennst.
Hinweis 2: Überlege dir welche Schleife am besten geeignet ist.
Hinweis 3: Versuche die Aufgabe zuerst ohne Berücksichtigung der Präzision zu lösen. Überlege dir dann, was die Bedingung für die gefordete Präzision sein könnte und wie du dies detektierst und dann die Berechnung abrichst.

Lösung:

#include <iostream>
int main () {
	double x;
	std::cin >> x;
	
	double numerator = x;
	double denominator = 1;
	
	double sum = x;
	double term;
	double term_abs;
	unsigned int n = 1;
	
	do {
		numerator *= -(x * x);
		denominator *= (2 * n) * (2 * n + 1);
		term = numerator / denominator;
		sum += term;
		if (term < 0) {
			term_abs = -term;
		} else {
			term_abs = term;
		}
		++n;
} while (term_abs > 0.000001);
 
std::cout << sum << std::endl;
return 0;
}