Algebra I Übung W04

Diedergruppen

Definition:
Wir definieren für $n\ge 3$ die Diedergruppe $D_n$ als

$$D_n=⟨r,s\mid r^n=s^2=1,srs=r^{-1}⟩.$$

Bemerkung: Diese Definition verwendet Notation, welche oft im Zusammenhang mit freien Gruppen eingeführt wird. Mit $⟨x,y⟩$ meint man, die freie nicht-abelsche Gruppe in zwei Erzeugern $x,y$. Diese besteht dann aus allen endlichen Wörter in $x,x^{-1},y,y^{-1}$ ($⟨x,y⟩=\left\{1,x,y,x^{-1},y^{-1},xx,xy,yx,yy,x{y}^{-1},y^{-1}x,x^{-1}{x}^{-1},\dots \right\})$. In unserem Fall betrachten wir nicht eine freie Gruppe, sonder eine mit den Relationen $r^n=s^2=1$ und $srs=r^{-1}$. Man kann sich das so vorstellen, dass man wieder alle endlichen Wörter betrachtet aber diesmal darf man mit den gegebenen Relationen “kürzen”. Betrachten wir zum Beispiel das endliche Wort $rrrsrs$. Durch Zusammenfassen mittels Exponenten erhalten wir $r^{3}srs$ und bemerken, dass wir die zweite Relation anwenden können. Wir erhlaten $r^{3}srs=r^3{r}^{-1}=r^2$. Durch weiteres ausprobieren sieht man, dass

$$D_n=\left\{1,r,r^2,\dots ,r^{n-1},s,rs,r^{2}s,\dots ,r^{n-1}s\right\},$$

und somit $|D_n|=2n$. Diese Definition ist äquivalent zu der geometrischen Definition aus der Vorlesung. Durch obige auflistung der Elemente, sieht man diese äquivalenz relativ gut. Die Elemente $1,r,\dots ,r^{n-1}$ entsprechen den Drehungen um $0,\frac{2\pi }{n},\dots ,(n-1)\cdot \frac{2\pi }{n}$ und die Elemente $s,rs,\dots ,r^{n-1}s$ entsprechen den $n$ Spiegelungen. Im folgender Abbildung sind die Spiegelungen als gestrichelte Linien für die Fälle $n=3,4,5,6$ eingezeichnet.

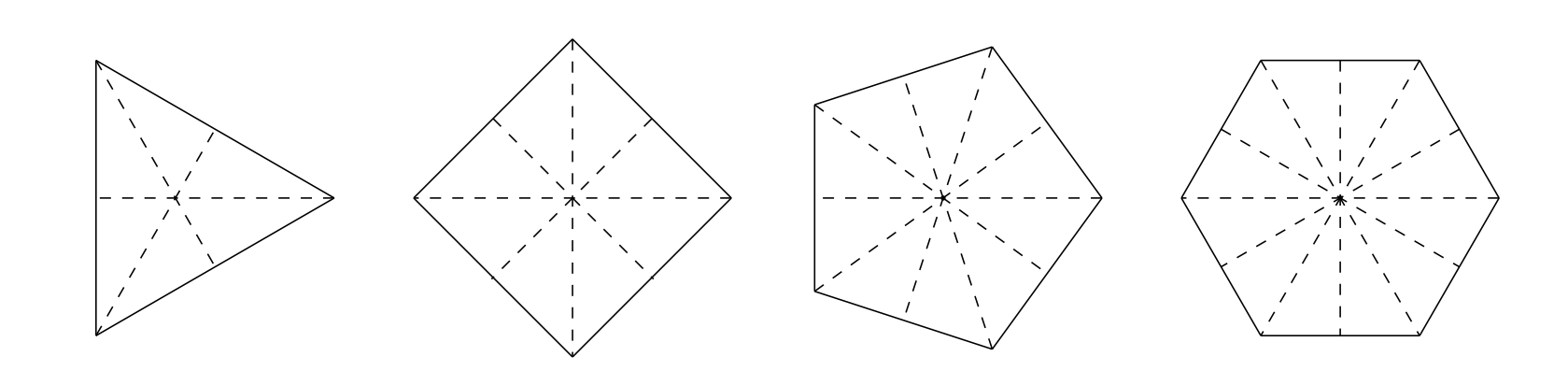
Gruppenoperation

Definition:
Sei $G$ eine Gruppe und $M$ eine Menge. Dann ist die Abbildung

$$\begin{array}{rl}G\times M& \to M\\ (a,x)& \mapsto a\circ x\end{array}$$

eine Operation von G auf M (kurz Operation/Gruppenoperation), falls gilt:
(1) $\forall x\in M:e_G\circ x=x$
(2) $\forall a,b\in G\forall x\in M:(ab)\circ x=a\circ (b\circ x)$

Beispiel:
Eine, nach obiger Diskusion, sehr natürliche Gruppenoperation ist die Operation von $D_n$ auf den Ecken eines regelmässigen $n$-Ecks. Wir betrachten als konkretes Beispiel den Fall $n=5$. Sei also

$$D_5=⟨r,s\mid r^5=s^2=1,srs=r^{-1}⟩=\left\{1,r,r^2,r^3,r^4,s,rs,r^{2}s,r^{3}s,r^{4}s\right\}.$$

Welcher geometrischen Operation entspricht das Element $r^{2}s$?

Wir sehen, dass jedes Element $g\in D_5$ einer Permutation der Ecken entspricht, also einem Element aus $S_5$. In anderen Worten entspricht jedes Gruppenelement einer Symmetrie des Pentagons. Das ist die historische Motivation der Gruppentheorie, die Lehre der Symmetrien. Bevor wir zu einem von diesem Beispiel motivierten Satz kommen, wollen wir uns noch ein paar Fragen zu diesem Beispiel stellen.

(1) Wie viele Bahnen hat diese Operation?
Wir bemerken, dass wir durch Rotation alleine schon von jedem Eckpunkt zu jedem anderen gelangen können. Wir haben also genau eine Bahn (eine Gruppenoperation mit dieser Eigenschaft nennt man transitiv).

(2) Wie sehen die Stabilistatoren aus?
Sei $x\in \left\{1,\dots ,5\right\}$ ein beliebiger Eckpunkt. Mit obiger Darstellung sehen wir es genau Elemente aus $D_5$ gibt, welche $x$ fixieren, das Neutralelement und die Spiegelung durch $x$. Wir erhalten somit zum Beispiel

$${\mathrm{Stab}}_{D_5}(1)=\left\{e,rs\right\},{\mathrm{Stab}}_{D_5}(2)=\left\{e,r^{3}s\right\}.$$

Da alle Eckpunkte in der selben Bahn liegen, sind deren Stabilisatoren konjugiert zu einander. Es gilt zum Beispiel $r\circ 1=2$ und somit

$$\begin{array}{rl}r{\mathrm{Stab}}_{D_5}(1)r^{-1}& =r\left\{e,rs\right\}{r}^{-1}\\ & =\left\{e,r^{2}s{r}^{-1}\right\}\\ r^{-1}=srs& =\left\{e,r^{2}s(srs)\right\}\\ & =\left\{e,r^{3}s\right\}\\ & ={\mathrm{Stab}}_{D_5}(2).\end{array}$$

Bemerkung:
Lässt man die Würfelgruppe $C$ auf den inneren vier Diagonalen des Würfels operieren, so sieht man analog zu oben, dass $C\cong S_4$.

Satz: (Cayley)
Sei $G$ eine endliche Gruppe der Ordnung $n$. Dann ist $G$ isomorph zu einer Untergruppe von $S_n$.

Beweis:
Wir lassen $G$ auf sich selbst durch linkstranslation operieren. Wie betrachten also folgende Gruppenoperation

$$\begin{array}{rl}G\times G& \to G\\ (g,x)& \mapsto gx.\end{array}$$

Man überprüft, dass dies tatsächlich eine Operation definiert. Wir wissen aus der Vorlesung, dass diese Operation einen Homomorphismus

$$\begin{array}{rl}\phi :G& \to S(G)\\ g& \mapsto {\pi }_g,\end{array}$$

wobei ${\pi }_g(x):=gx$ für alle $x\in G$. Per Annahme gilt $|G|=n$ und somit $S(G)\cong S_n$ als Gruppen. Des weiteren gilt falls $\phi (g)=\phi (h)$ für $g,h\in G$, dann gilt ${\pi }_g(e)={\pi }_h(e)$ und somit $g=h$. Dies zeigt Injektivität von $\phi$ und wir erhalten somit den Isomorphismus $\phi :G\to \phi (G)\le S(G)\cong S_n$.

$$\begin{array}{r}\end{array}\text{\hspace{1em}□}$$

Proposition: (aus der Vorlesung)
Sei $G\curvearrowright M$ eine Gruppenoperation. Dann gilt
(a) $\forall x\in M$ gilt ${\mathrm{St}}_G(x)\le G$
(b) $M={⨆}_{N\in M/G}N$ (disjunkte Vereingung)
(c) $\forall x\in M\forall a\in G:{\mathrm{St}}_G(a\circ x)=a{\mathrm{St}}_G(x)a^{-1}$
(d) $\forall x\in M:[G:{\mathrm{St}}_G(x)]=|Gx|$

Beispiel:
Wir wollen uns nun noch ein weiteres Beispiel einer Gruppenoperation anschauen. Wir fixieren ein $n\in {\mathbb{N}}_{\ge 1}$ und betrachten $\mathbb{Z}$ als additive Gruppe und die Menge

$$S^1:=\left\{z\in \mathbb{C}\mid |z|=1\right\}.$$

Wir definieren

$$\begin{array}{rl}\mathbb{Z}\times S^1& \to S^1\\ (k,z)& \mapsto k\circ z=e^{2\pi ik/n}z.\end{array}$$

Wir bemerken zuerst, dass obige Funktion wohldefiniert ist, da $|e^{2\pi ik/n}|=1$ für beliebiges $k\in \mathbb{Z}$. Nun, wollen wir überprüfen, dass obiges eine Gruppenoperation definiert. Seien dafür $z\in S^1$ und $k,\ell \in \mathbb{Z}$ beliebig, dann gilt

$$0\circ z=e^{0}z=z$$

und

$$(k+\ell )\circ z=e^{2\pi i(k+\ell )/n}z=e^{2\pi ik/n}{e}^{2\pi i\ell /n}z=k\circ (\ell \circ z).$$

Geometrisch handelt es sich bei dieser Operation um eine Rotation des Einheitskreises $S^1$, wobei $k\in \mathbb{Z}$ eine Rotation um $\frac{2\pi k}{n}$ induziert. Im Falle $n=4$:

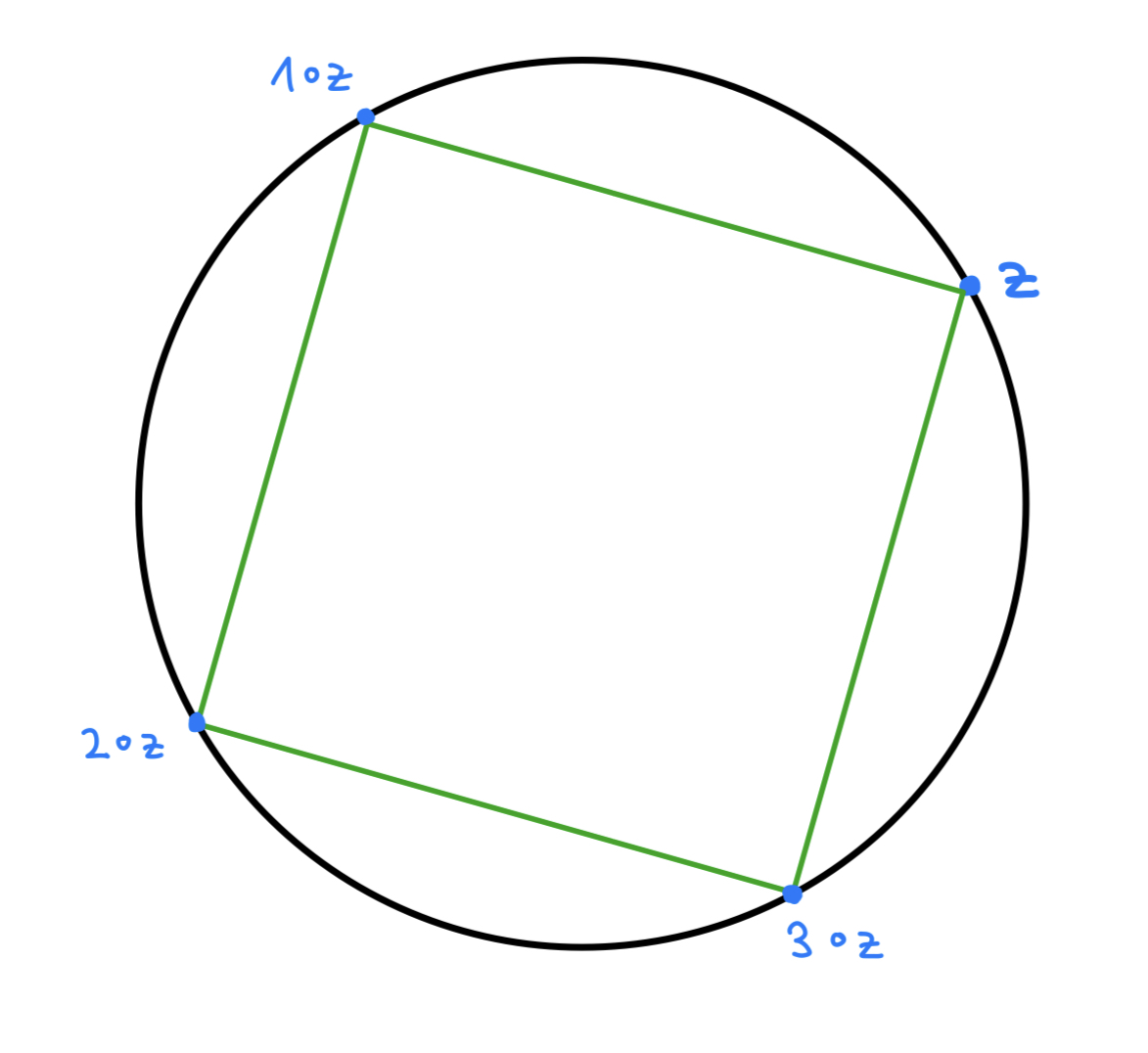
Und hier sind vier verschiedene Orbits für den Fall $n=3$ eingezeichnet.

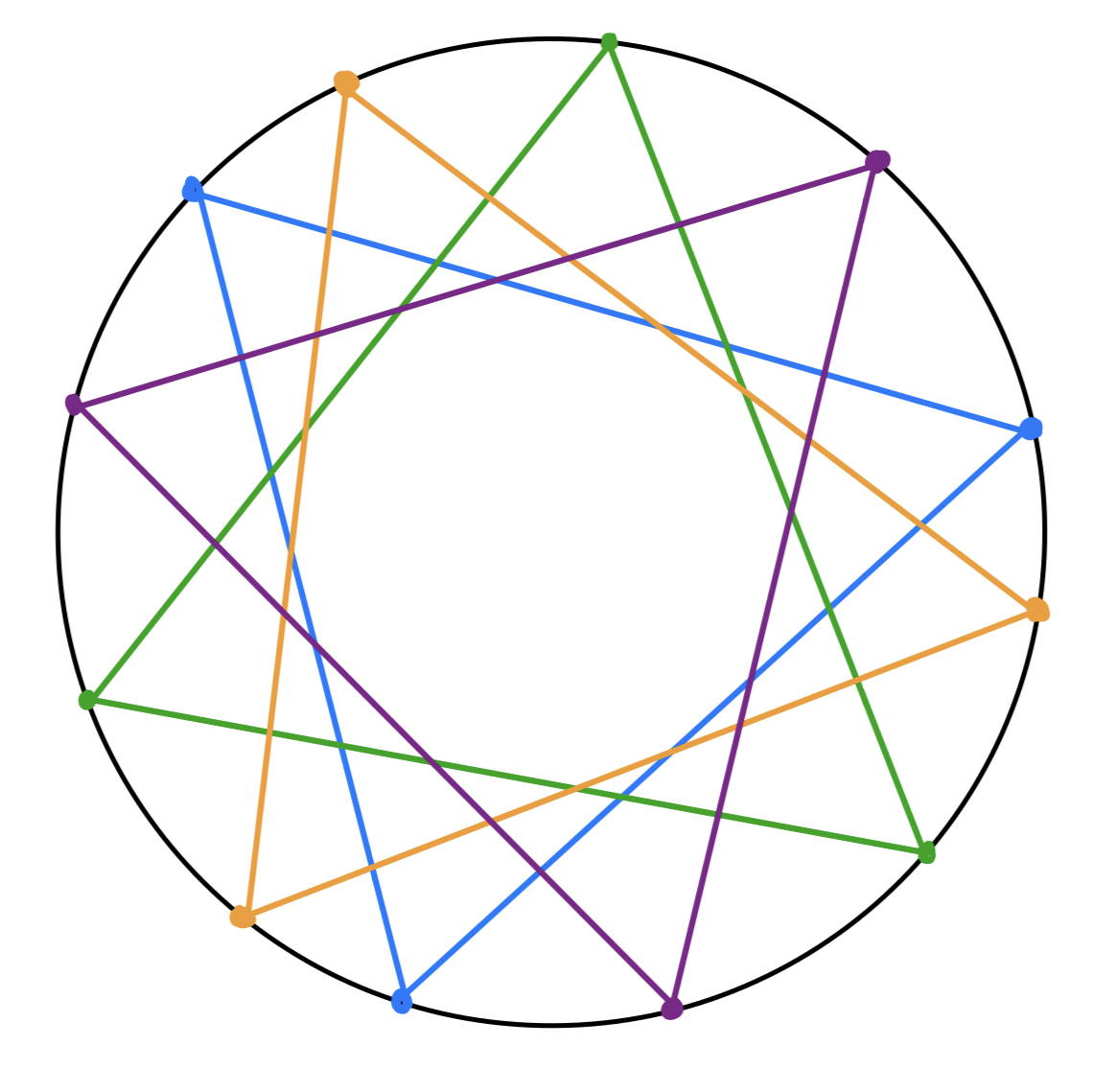
Sei $z\in S^1$ beliebig. Wir wollen die Bahn von $z$ beschreiben. Es gilt

$$\begin{array}{rl}\mathbb{Z}z& =\left\{k\circ z\mid k\in \mathbb{Z}\right\}\\ & =\left\{e^{2\pi ik/n}z\mid k\in \mathbb{Z}\right\}\\ e^{2\pi i}=1& =\left\{e^{2\pi ik/n}z\mid k\in \left\{0,\dots ,n-1\right\}\right\}.\end{array}$$

Dies ergibt intuitiv auch Sinn, wenn ich $z$ wiederholt um $\frac{2\pi }{n}$ rotiere, lande ich nach $n$ Rotationen wieder auf $z$. Es gilt also $|\mathbb{Z}z|=n$ für alle $z\in S^1$. Wir wollen nun den Stabilisator beschreiben. Sei wieder $z\in S^1$ beliebig, dann

$$\begin{array}{rl}{\mathrm{St}}_{\mathbb{Z}}(z)& =\left\{k\in \mathbb{Z}\mid k\circ z=z\right\}\\ & =\left\{k\in \mathbb{Z}\mid e^{2\pi ik/n}z=z\right\}\\ e^{2\pi ik/n}=1⟺n|k& =n\mathbb{Z}.\end{array}$$

Da der Stabilisator unabhängig von $z$ ist folgt mit Teil (c) aus obiger Propisition

$$n\mathbb{Z}=k(n\mathbb{Z})k^{-1}$$

für alle $k\in \mathbb{Z}$. Dies impliziert, dass $n\mathbb{Z}$ ein Normalteiler von $\mathbb{Z}$ ist (was auch direkt daras folgt, dass es eine Untergruppe ist und $\mathbb{Z}$ abelsch ist). Des weiteren, wissen wir für $z\in S^1$

$$[\mathbb{Z}:{\mathrm{St}}_{\mathbb{Z}}(z)]=[\mathbb{Z}:n\mathbb{Z}]=n=|\mathbb{Z}z|,$$

was Teil (d) aus obiger Proposition entspricht.

Mit $\alpha \in \mathbb{R}\setminus \mathbb{Q}$ könnte man auch die analoge Gruppenoperation

$$\begin{array}{rl}\mathbb{Z}\times S^1& \to S^1\\ (k,z)& \mapsto k\circ z=e^{2\pi i\alpha k}z,\end{array}$$

die Rotation um ein irrationales Vielfache von $2\pi$, betrachten. Man kann zeigen, dass die Stabilisatoren trivial sind und dass jeder Orbit dicht in $S^1$ ist.

Bemerkung:
Wir haben in der Vorlesung gesehen, dass falls $H\le G$ mit $[G:H]=2$, dann folgt $H⊴G$. Wir wollen nun eine Verallgemeinerung beweisen.

Proposition:
Sei $G$ eine endliche Gruppe. Sei $p$ der kleinste Primfaktor von $|G|$ und $H\le G$ mit $[G:H]=p$. Dann gilt $H⊴G$.

Beweis:
Wir betrachten die Gruppenoperation

$$\begin{array}{rl}H\times G/H& \to G/H\\ (h,xH)& \mapsto h\circ xH=hxH.\end{array}$$

Wir bemerken, dass die Bahn von $H\in G/H$ nur aus einem Element besteht, da $hH=H$ für alle $h\in H$. Aus Teil (b) der obigen Proposition und da $|G/H|=[G:H]=p$ folgt, dass die anderen Bahnen maximal Länge $p-1$ haben. Aus Teil (d) der obigen Proposition folgt, dass die Länge der Bahnen $|H|$ teilt und somit auch $|G|$ teilt. Da $p$ der kleinste Primfaktor von $|G|$, haben somit alle Bahnen Länge 1. Das heisst, $\forall h\in H\forall x\in G$ gilt

$$h\circ xH=xH$$

und somit $hxH=xH$, was wiederrum $x^{-1}hxH=H$ impliziert. Aufgrund der Eigenschaften von Nebenklassen (Proposition aus letzter Woche) folgt nun $x^{-1}hx\in H$. Da $h\in H,x\in G$ beliebig waren folgt $H⊴G$.

$$\begin{array}{r}\end{array}\text{\hspace{1em}□}$$