Algebra I, MC10

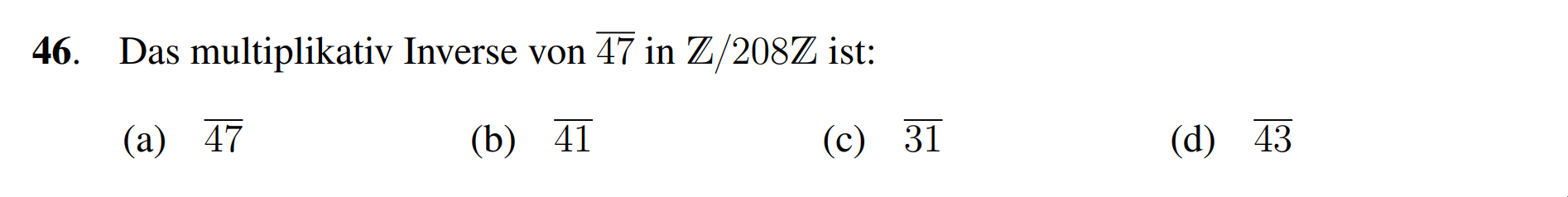
Wir wenden den Euklidischen Algorithmus and und finden

$$\begin{array}{ccccccc}\begin{array}{rl}208& =4\cdot 47+20\\ 47& =2\cdot 20+7\\ 20& =2\cdot 7+6\\ 7& =1\cdot 6+1\\ 6& =6\cdot 6+0\end{array}& & & & & & \begin{array}{cccccc}& 4& 2& 2& 1& 6\\ 1& 0& 1& -2& 5& -7\\ 0& 1& -4& 9& -22& 31\end{array}\end{array}$$

Es folgt $-7\cdot 208+31\cdot 47=1$ und somit $47^{-1}\equiv 31\mathrm{mod}208$. Die richtige Antwort ist also (c).

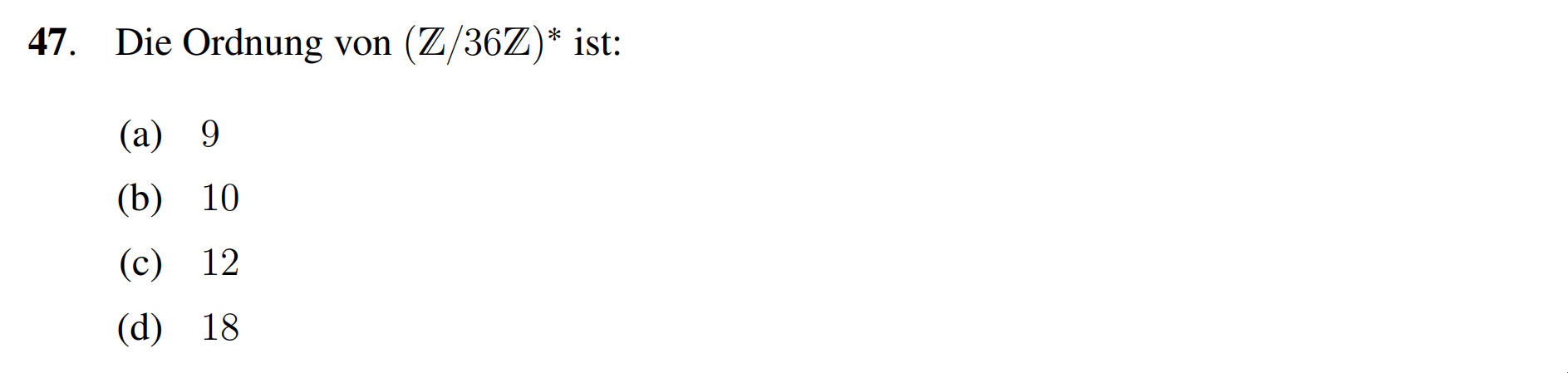
Wir nutzen die multiplikativität der Euler $\phi$ Funktion und erhalten

$$\begin{array}{rl}\phi (36)& =\phi (2^2)\phi (3^2)\\ & =(2^2-2)(3^2-3)\\ & =12.\end{array}$$

Es folgt Antwort (c).

Wir bemerken, dass $\phi (37)=36$ also hat die multiplikative Gruppe $(\mathbb{Z}/37\mathbb{Z}{)}^{\ast }$ Ordnung 36. Nun folgt

$$\begin{array}{rl}{2}^{36}& \equiv 1\mathrm{mod}37\\ 17^{36}& \equiv 1\mathrm{mod}37\\ (13^{37}{)}^{37}& \equiv 13^{37}\equiv 13\mathrm{mod}37\\ (45^{37}{)}^{37}& \equiv 45\equiv 8\mathrm{mod}37,\end{array}$$

wobei wir lediglich verwendent haben, dass die Ordnungen der Elementen von $(\mathbb{Z}/37\mathbb{Z}{)}^{\ast }$ Teiler von 36 sind. Es folgt, dass (b) und (d) richtig sind.

Wir wollne die Operation genauer Untersuche. Wir bemerken zuerst, dass $|A_5|=2^2\cdot 3\cdot 5$ und da $H\cong C_5$ erhalten wir, dass $H\in {\mathrm{Syl}}_5(A_5)$. Mit Sylow folgt

$$\{\begin{array}{l}|{\mathrm{Syl}}_5(A_5)||12\\ |{\mathrm{Syl}}_5(A_5)|\equiv 1\mathrm{mod}5.\end{array}$$

Da wir wissen, dass $A_5$ einfach ist, folgt $|{\mathrm{Syl}}_5(A_5)|=6$. Da bedeutet, dass die Bahn $A_5(H)$ von $H$ aus genau 6 Elementen besteht. Wegen $|A_5(H)|=[A_5:{\mathrm{St}}_{A_5}(H)]$ folgt $|{\mathrm{St}}_{A_5}(H)|=10$. Wir wollen noch die Struktur von ${\mathrm{St}}_{A_5}(H)$ bestimmen. Wir suchen also Untergruppen der Ordnung 10 in $A_5$. Mit Aufgabe 46 aus Serie 8 oder einfachmit Sylow + äussere Produkte folgt, dass es bis auf Isomorphie nur die Gruppen $C_{10}$ und $D_5$ der Ordnung 10 gibt. Da $C_{10}$ einem 10-Zykel entsprechend würde und es solche in $A_5$ nicht gibt, muss es $D_5$ sein. Also ${\mathrm{St}}_{A_5}(H)\cong D_5$. Es folgt, dass (a), (c) und (d) richtig sind.

Wir zeigen Inklusionen der adjungierten Elemente.
(a) $\subseteq$ (b): Da $3\cdot \frac{1}{6}=\frac{1}{2}$ und $2\cdot \frac{1}{6}=\frac{1}{3}$, können wir jedes Element von $\mathbb{Z}\left[\frac{1}{2},\frac{1}{3}\right]$ auch in $\mathbb{Z}\left[\frac{1}{6}\right]$ darstellen.
(b) $\subseteq$ (c): Da $2\cdot \frac{1}{12}=\frac{1}{6}$, folgt $\mathbb{Z}\left[\frac{1}{6}\right]\subseteq \mathbb{Z}\left[\frac{1}{12}\right]$.
(c) $\subseteq$ (a): Da $\frac{1}{2}\cdot \frac{1}{2}\cdot \frac{1}{3}=\frac{1}{12}$, folt $\mathbb{Z}\left[\frac{1}{12}\right]\subseteq \mathbb{Z}\left[\frac{1}{2},\frac{1}{3}\right]$.

Dies zeigt $\mathbb{Z}\left[\frac{1}{2},\frac{1}{3}\right]=\mathbb{Z}\left[\frac{1}{6}\right]=\mathbb{Z}\left[\frac{1}{12}\right]$. Schlussentlich bemerken wir noch, dass $6\cdot \frac{1}{30}=\frac{1}{5}\in \mathbb{Z}\left[\frac{1}{30}\right]$, aber $\frac{1}{5}$ lässt sich in keinen der anderen Ringe darstellen. Es folgt (d).

Eine genaurer Begründung für den letzten Schritt wäre die Folgende.
Behauptung: $\mathbb{Z}\left[\frac{1}{6}\right]=\left\{\frac{k}{6^n}\mid k\in \mathbb{Z}\text{ und }n\in \mathbb{N}\right\}$.

Angenommen $\frac{1}{5}\in \mathbb{Z}\left[\frac{1}{6}\right]$, dann gilt $\frac{1}{5}=\frac{k}{6^n}$ für ein $k\in \mathbb{Z}$ und $n\in \mathbb{N}$. Dies würde aber implizieren, dass $5|6^n$. Ein Widerspruch.

Beweis der Behauptung:
Es ist nicht schwer zu zeigen, dass die rechte Seite ein Unterring bildet, welcher in $\mathbb{Z}\left[\frac{1}{6}\right]$ enthalten ist. So folgt dann per Definition von $\mathbb{Z}\left[\frac{1}{6}\right]$ als kleinster Unterring von $\mathbb{R}$, welcher $\mathbb{Z}$ und $\frac{1}{6}$ enthält, die gewünschte Gleichheit.