Algebra I, MC08

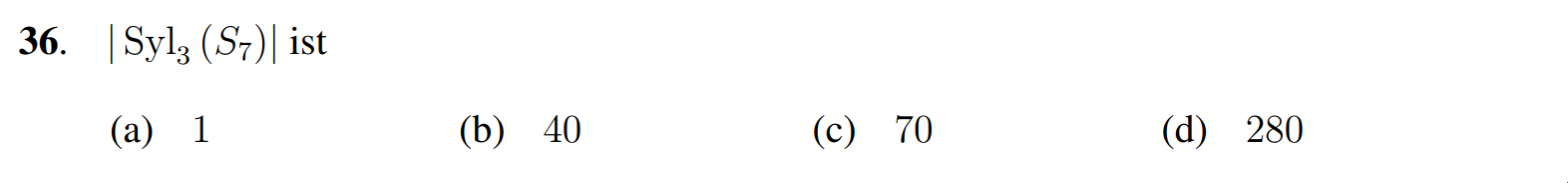
Eine erste Idee wäre Sylow zu verwenden. Wir bemerken zuerst, dass $|S_7|=2^4\cdot 3^2\cdot 5\cdot 7$ gilt, also liefert Sylow

$$\{\begin{array}{l}|{\mathrm{Syl}}_3(S_7)||2^4\cdot 5\cdot 7\\ |{\mathrm{Syl}}_3(S_7)|\equiv 1\mathrm{mod}3.\end{array}$$

Wir sehen, dass uns dies nicht viel weiter bringt. Wir können zum Beispiel $2^3$, $2^3\cdot 7$, $5\cdot 7$, usw. aufgrund derer Kongruenzklasse modulo 3 auschliessen, aber haben immernoch viele mögliche Optionen $2^2$, $2^4$, $2^4\cdot 7$, $2^3\cdot 5$, usw. Wir müssen irgendwie die Struktur von $S_n$ nutzen.

Wir bemerken, dass die eine Sylow 3-Untergruppe in $S_7$ Ordnung $3^2$ hat ($p^2$ für $p$ prim), also ist diese abelsch. Somit haben wir bis auf Isomorphie nur zwei Möglichkeiten $C_9$ oder $C_3\times C_3$. Eine Permutation der Ordnung $p^2$ muss einen $p^2$-Zykel in der Zerlegung in disjunkte Zykel enthalten (wieso?), somit besitzt $S_7$ keine Permutationen der Ordnung 9. Es folgt, dass die Sylow 3-Untergruppen in $S_7$ Isomorph zu $C_3\times C_3$ sind. Wir bemerken, dass jedes $P\in {\mathrm{Syl}}_3(S_7)$ zwei disjunkten 3-Zykel ensptricht und umgekehrt entsprechen zwei disjunkte 3-Zykel einer Sylow 3-Untetrgruppe. Falls $\sigma ,\rho$ zwei solche disjunte 3-Zykel sind, dann gilt

$$C_3\times C_3\cong ⟨\sigma ,\rho ⟩=\left\{\iota ,\sigma ,\rho ,{\sigma }^{-1},{\rho }^{-1},\sigma \rho ,\sigma {\rho }^{-1},{\sigma }^{-1}\rho ,{\sigma }^{-1}{\rho }^{-1}\right\}.\text{\hspace{1em}(⋆)}$$

Frage: Wie viele $m$-Zykel gibt es in $S_n$?
Falls $m>n$, dann keine. Falls $m\le n$, dann gibt es $\left(\genfrac{}{}{0ex}{}{n}{m}\right)$ Teilmengen $A\subseteq [n]:=\left\{1,\dots ,n\right\}$ mit $|A|=m$. Gegeben eine solche Teilmenge gibt es $m!$ Arten diese Elementen in einem Zykel anzuordnen, aber

$$(123)=(231),$$

also sind nicht alle $m!$ verschieden. Für einen $m$-Zykel gibt es immer genau $m$ Arten diesen zu schreiben, da jedes Element an der ersten Stelle stehen kann. Es gibt also $(m-1)!$ verschiedene $m$-Zykel auf der Menge $A$. Es folgt, dass es insgesamt

$$\left(\genfrac{}{}{0ex}{}{n}{m}\right)(m-1)!$$

verschiedene $m$-Zykel in $S_n$ gibt.

Es existieren also genau $\left(\genfrac{}{}{0ex}{}{7}{3}\right)2=70$ verschiedene 3-Zykel in $S_7$. Angenommen wir fixieren einen solche 3-Zykel $\sigma \in S_7$. Dann zeigt obiges argument, dass es genau $\left(\genfrac{}{}{0ex}{}{4}{3}\right)2=8$ 3-Zykel $\rho \in S_7$ gibt, welche disjunkt zu $\sigma$ sind. Wir erhalten also $70\cdot 8=560$ Paare von disjunkten $3$-Zykel. Wir bemerken schlussendlich, dass

$$\begin{array}{cccc}\sigma ,\rho & \rho ,\sigma & {\sigma }^{-1},\rho & {\rho }^{-1},\sigma \\ \sigma ,{\rho }^{-1}& \rho ,{\sigma }^{-1}& {\sigma }^{-1},{\rho }^{-1}& {\rho }^{-1},{\sigma }^{-1}\end{array}$$

alle die selbe zu $C_3\times C_3$ isomorphe Untergruppe in $S_7$ erzeugen (siehe $(\star )$). Es gibt also $\frac{70\cdot 8}{8}=70$ verschiedene zu $C_3\times C_3$ isomorphe Untergruppen in $S_7$. Die richtige Antwort ist somit (c).

(a) Richtig, nach obiger Diskussion sind diese entweder isomorph zu $C_4$ oder $C_2\times C_2$. Da aber jeder 4-Zykel ungerade ist, sind diese nicht in $A_5$ enthalten. Somit muss es $C_2\times C_2$ sein.
(b) Richtig, es gilt $|S_{14}|=14!=7^2\cdot n$ für ein $n\in \mathbb{N}$ mit $7\nmid n$. Da alle Gruppen der Ordnung $p^2$ für $p$ prim abelsch sind folgt die Aussage.
(c) Richtig, die Sylow 7-Untergruppen von $S_7$ haben Ordnung $7$, also sind diese zyklisch.
(d) Falsch, siehe (e)
(e) Richtig, wir wissen, dass $S_4$ zu $D_4$ isomorphe Untergruppen enthält. Da $S_4\le S_5$ besitzt $S_5$ also auch zu $D_4$ isomorphe Untergruppen. Da die Sylow 2-Untergruppen von $S_5$ Ordnung 8 haben folgt die Aussage.

(a) Richtig, die Sylow $p$-Untergruppen haben Ordnungen 2, 7 oder 11, also sogar zyklisch.
(b) Falsch, da $|D_8\times C_{11}|=2^4\cdot 11$ habe die Sylow 2-Untergruppen Ordnung 16. $D_8$ is eine solche Untergruppe aber nicht abelsch.
(c) Richtig, die Sylow $p$-Untergruppen haben Ordnungen $p$ oder $p^2$, also abelsch.
(d) Richtig, wir bemerken $|D_{14}\times D_7|=2^3\cdot 7^2$. Für $p=7$ ist es klar, da alle Gruppen der Ordnung $p^2$ für $p$ prim abelsch sind. Wir müssen nun noch $p=2$ prüfen. Sei $P$ eine Sylow 2-Untergruppe von $D_{14}$ und $Q$ eine Sylow 2-Untergruppe von $D_7$. Da diese Ordnunge $2^2$ respektive $2$ haben sind diese abelsch. Wir bemerken, dass $P\times Q$ eine Sylow 2-Untergruppe von $D_{14}\times D_7$ ist. Da $P\times Q$ abelsch ist und alle Sylow $2$-Untergruppen isomorph zueinander sind folgt die Aussage.

(a) Richtg, wir wissen, dass die 3-Zykel $A_6$ erzeugt. Fügen wir nun noch $(12)$ hinzu, so erhalten wir auch alle ungeraden Permutationen also ganz $S_6$.
(b) Richtig, wir wollen zuerst das Erzeugnis von allen 5-Zyklen verstehen. Zuerst bemerken wir, dass die Konjugation eines 5-Zykel wieder ein 5-Zykel gibt. Somit ist die Menge alle 5-Zykel $S$ invariant unter Konjugation. So gilt aber auch, dass $⟨S⟩$ invariant under Konjugation ist, denn $\pi ⟨S⟩{\pi }^{-1}=⟨\pi S{\pi }^{-1}⟩=⟨S⟩$. Also gilt $⟨S⟩⊴S_6$. Da die 5-Zykel gerade sind gilt $⟨S⟩⊴A_{{}_6}$. Da $A_6$ einfach ist folgt $⟨S⟩=A_6$. Wenn wir nun die ungerade Permutation $(1256)$ noch betrachten, dass erhalten wir zusätzlich noch ungerade Permutationen. Da $A_6$ die grösse echte Untergruppe von $S_6$ ist ($[S_6:A_6]=2$) folgt $⟨S,(1256)⟩=S_6$.
(c) Richtig, siehe (b).
(d) Falsch, wir wissen, dass die 3-Zykel $A_6$ erzeugen.

Wir bemerken zuerst, dass ${\pi }^{-1}=(76542)$ und ${\rho }^{-1}=(27351)$. Mit dem Lemma über Konjugation von Zykel erhalten wir

$$\begin{array}{rl}{\rho }^{-1}\pi \rho & =({\rho }^{-1}(2){\rho }^{-1}(4){\rho }^{-1}(5){\rho }^{-1}(6){\rho }^{-1}(7))\\ & =(74163)\\ & =(63741)\end{array}$$

Analoge Rechnungen zeigen

$$\begin{array}{rl}\rho \pi {\rho }^{-1}& =(\rho (2)\rho (4)\rho (5)\rho (6)\rho (7))\\ & =(14362)\\ & =(36214)\end{array}$$

und

$$\begin{array}{rl}\rho {\pi }^{-1}{\rho }^{-1}& =(26341)\\ & =(34126).\end{array}$$

Somit sind nur (a) falsch.