Algebra I, MC07

Wir haben in der letzten Übungsstunde gesehen, dass sich das Problem auf die Partitionen der 5 reduzieren lässt. Wir finden

$$\begin{array}{rl}5& =4+1\\ & =3+2\\ & =3+1+1\\ & =2+2+1\\ & =2+1+1+1\\ & =1+1+1+1+1\end{array}$$

Es gibt also bis auf Isomorphie die folgenden 7 abelsche Gruppen der Ordnung $7^5$.

$$\begin{array}{c}{C}_{7^5}\\ C_{7^4}\times C_7\\ C_{7^3}\times C_{7^2}\\ C_{7^3}\times C_7\times C_7\\ C_{7^2}\times C_{7^2}\times C_7\\ C_{7^2}\times C_7\times C_7\times C_7\\ C_7\times C_7\times C_7\times C_7\times C_7.\end{array}$$

Die richtige Antwort ist also (c).

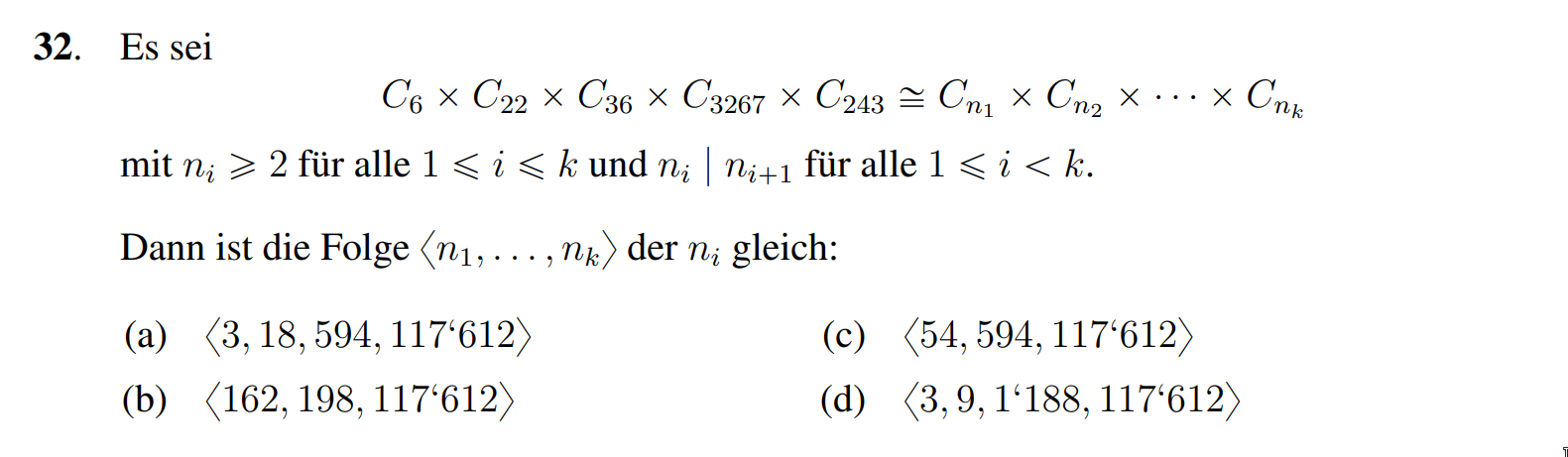
Wir folgen dem Algorithmus aus letzter Übungsstunde. Wir finden folgende Primfaktorzerlegungen:

$$\begin{array}{rl}6& =2\cdot 3\\ 22& =2\cdot 11\\ 36& =2^2\cdot 3^2\\ 3267& =3^3\cdot 11^2\\ 243& =3^5.\end{array}$$

Also

$$\begin{array}{cccccc}\text{Primzahl}& & & & & \\ 2& 2^2& 2& 2& 1& 1\\ 3& 3^5& 3^3& 3^2& 3& 1\\ 11& 11^2& 11& 1& 1& 1\\ \text{Produkt der Spalten}& 117^{\prime }612& 594& 18& 3& 1\end{array}$$

Es folgt (a).

(a) Richtig, wir haben in der Vorlesung gezeigt, dass eine Gruppe der Ordnung $p^2$ immer abelsch ist. Mit dem Haupsatz über endlich erzeugt abelsche Gruppe folgt dann (da es genau zwei Partitionen der 2 gibt), dass es bis auf Isomorphie genau zwei Gruppen der Ordnung $p^2$ gibt.
(b) Falsch, wir haben in der Vorlesung gezeigt, dass eine Gruppe der Ordnung $p^2$ immer abelsch ist.
(c) Richtig, jede abelsche Gruppe ist auflösbar. In Aufgabe 33 der Serie 5 wurde sogar gezeigt, dass jede Gruppe der Ordnung $p^n$ für $p$ prim und $n\ge 0$ auflösbar ist.

(a) Richtig, nach Sylow sind alle Sylow $p$-Untergruppen Isomorph zueinander. Da die Untergruppe $H$ eine Sylow $11$-Untergruppe bilden würde folgt die Aussage.
(b) Richtig, nach Sylow hat die Gruppe $G$ eine 11-Sylowuntergruppe. Also eine Untergruppe der Ordnung $121$. Diese hat Index $2$ in $G$, also ist sie normal. Somit besitzt $G$ immer eine nicht-triviale normale Untergruppe.
(c) Falsch, (b)
(d) Falsch, $D_{121}$ ist ein Gegenbeispiel.

Wir bemerken $|S_4|=24=2^3\cdot 3$ und wenden das Sylowtheorem für $p=2$ an. Es folgt

• $|{\mathrm{Syl}}_2(S_4)|\equiv 1\mathrm{mod}2$
• $|{\mathrm{Syl}}_2(S_4)||3$

Wir erhalten insgesamt also $|{\mathrm{Syl}}_2(S_4)|\in \left\{1,3\right\}$. Nehmen wir per Widerspruch an, dass $|{\mathrm{Syl}}_2(S_4)|=1$. So ist $P\in {\mathrm{Syl}}_2(S_4)$ normal. Sei nun $(ij)$ eine beliebige Transposition in $S_4$. Sei $H=⟨(ij)⟩$. Dann gilt $|H|=2$ und da $P$ normal ist $PH\le G$. Des weiteren haben wir

$$|PH|=\frac{|P||H|}{|P\cap H|}=2^k$$

für ein $k\in \mathbb{N}$. Da $P\le PH$ folgt $k=3$ und somit $P=PH$. Dies zeigt insbesondere $(ij)\in P$. Da $(ij)$ eine beliebige Transposition war und diese die ganze Gruppe $S_4$ erzeugen, folgern wir $P=S_4$. Ein Widerspruch. Somit gilt $|{\mathrm{Syl}}_2(S_4)|=3$ (c).