Algebra I, MC06

Wir wollen diese Operation besser verstehen. Dazu wollen wir zuerst die Bahn des Elements $\left(\begin{array}{c}1\\ 0\end{array}\right)$ betrachten. Sie $\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in {\mathrm{GL}}_2(\mathbb{Q})$, dann gilt

$$\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\circ \left(\begin{array}{c}1\\ 0\end{array}\right)=\left(\begin{array}{c}a\\ c\end{array}\right).$$

Wir sehen, dass wir nur Punkte mit rationalen Koordinaten von $\left(\begin{array}{c}1\\ 0\end{array}\right)$ aus erreichen können (da $a,c\in \mathbb{Q}$). Also folgt $G\left(\begin{array}{c}1\\ 0\end{array}\right)\subseteq {\mathbb{Q}}^2$. Indem wir jedoch $d=0$ und $b=\frac{1}{a}$ oder $b=0$ und $d=\frac{1}{c}$, je nach dem ob $a\ne 0$ oder $b\ne 0$, sehen wir, dass ${\mathbb{Q}}^2\setminus \left\{(0,0)\right\}\subseteq G\left(\begin{array}{c}1\\ 0\end{array}\right)$. Da für alle $A\in G$ gilt $A\circ \left(\begin{array}{c}0\\ 0\end{array}\right)=\left(\begin{array}{c}0\\ 0\end{array}\right)$, bildet der Urspung einen Fixpunkt und wir erhalten

$$G\left(\begin{array}{c}1\\ 0\end{array}\right)={\mathbb{Q}}^2\setminus \left\{(0,0)\right\}.$$

Also sind (b) und (c) sicherlich richtig. Wir haben bisher also zwei Bahnen klassifiziert. Da wir jedoch Punkte mit irrationalen Koordinaten nicht in diesen zwei Bahnen enthalten sind und die Bahnen die Menge ${\mathbb{R}}^2$ partitionieren, folgt (a).

Man könnte weiter gehen und sich fragen on man die Bahen irgendwie klassifieren kann und wie viele es gibt. Für $v=\left(\begin{array}{c}x\\ y\end{array}\right)\in {\mathbb{R}}^2$ definieren wir

$$U_v:=\left\{ax+by\mid a,b\in \mathbb{Q}\right\}\subseteq \mathbb{R}.$$

Behauptung: Für $v,w\in {\mathbb{R}}^2$ gilt $Gv=Gw$ genau dann, wenn $U_v=U_w$.

Wir betrachten $\mathbb{R}$ als Vektorraum über $\mathbb{Q}$. Dann entspricht $U_v$ genau dem von $x,y$ erzeugten Untervektorraum $⟨x,y⟩$. Weiter bemerken wir, dass die Menge $\left\{U_v\mid v\in {\mathbb{R}}^2\right\}$ mit den $0$-, $1$- und $2$-dimensionalen $\mathbb{Q}$-Unterräumen von $\mathbb{R}$ in Bijektion steht. Mit obiger Behauptung stehen also die Bahnen der Operation ${\mathrm{GL}}_2(\mathbb{Q})\curvearrowright {\mathbb{R}}^2$ in Bijektion mit den $0$-, $1$- und $2$- dimensionalen $\mathbb{Q}$-Untervektorräumen von $\mathbb{R}$. Des weiteren bemerken wir, dass ${\dim }_{\mathbb{Q}}\mathbb{R}=\infty$, womit also unendlich viele verschiedene Bahnen existieren.

Beweis der Behauptung:
Wir schreiben $v=\left(\begin{array}{c}x\\ y\end{array}\right)$ und $w=\left(\begin{array}{c}s\\ t\end{array}\right)$.

$⟹$:
Angenommen $Gv=Gw$. Dann existiert ein $A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in G$, so dass $A\circ v=w$. Durch ausschreiben der Matrixmultiplikation erhalten wir $ax+by=s$ und $cx+dy=t$. Es folgt $U_w\subseteq U_v$. Analog existiert ein $B\in G$, so dass $B\circ w=v$, was $U_v\subseteq U_w$ und somit Gleichheit impliziert.

$⟸$:
Sei $U:=U_v=U_w$. Wir unterscheiden drei Fälle:

Falls $\dim U=0$, so folgt $v=w=\left(\begin{array}{c}0\\ 0\end{array}\right)$ und somit die Implikation.

Falls $\dim U=1$, so gilt oBdA $U_v=⟨x⟩=⟨s⟩=U_w$. So existieren $\alpha ,\beta ,\gamma \in \mathbb{Q}$, so dass $y=\alpha x$, $s=\beta x$, $t=\gamma x$, wobei $\beta \ne 0$. So gilt für

$$A=\left(\begin{array}{cc}\beta & 0\\ \gamma -\alpha & 1\end{array}\right)\in {\mathrm{GL}}_2(\mathbb{Q})$$

gerade $A\circ v=w$. Es folgt $Gv=Gw$.

Falls $\dim U=2$. So bilden $x,y$ und $s,t$ zwei $\mathbb{Q}$-Basen $U$. So existieren also $a,b,c,d\in \mathbb{Q}$, so dass

$$\begin{array}{rl}ax+by& =s\\ cx+dy& =t.\end{array}$$

Für $A=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$ gilt also $A\circ v=w$. Es bleibt zu zeigen, das diese invertierbar ist. Angenommen $A$ ist nich invertierbar, dann sind die Zeilen von $A$ linear abhängig, also existiert ein $\alpha \in \mathbb{Q}$, so dass $\alpha a=c$ und $\alpha b=d$. So folgt aber $\alpha s=t$, ein Widerspruch zur $\mathbb{Q}$-linearen Unabhängigkeit von $s,t$.

$$\begin{array}{r}\end{array}\text{\hspace{1em}□}$$

(a) Richtig, $S_3\cong D_3=⟨r,s\mid r^3=s^2=e\text{ und }srs=r^{-1}⟩$
(b) Richtig, in Aufgabe 31 der Serie 5 habt ihr gesehen, dass $C$ von zwei Elementen erzeugt wird. Ihr werdet auch bald sehen, dass $S_n$ von $(12)$ und $(12\dots n)$ erzeugt wird für jedes $n\ge 2$.
(c) Richtig, $C_2\times C_3\cong C_6$ und wird somit sogar von nur einem Element erzgeugt.

Wir bemerken zuerst, dass weil es sich um ein direktes Produkt handelt folgende Äquivalenz gilt

$$\begin{array}{c}\left\{(a,0,0),(0,b,0),(0,0,c)\right\}\text{ erzeugt }\mathbb{Z}\times \mathbb{Z}\times \mathbb{Z}/7\mathbb{Z}\\ ⟺\\ ⟨a⟩=⟨b⟩=\mathbb{Z}\text{ und }⟨c⟩=\mathbb{Z}/7\mathbb{Z}.\end{array}$$

So sehen wir, dass $\left\{(1,0,0),(0,1,0),(0,0,\overline{1})\right\}$ die Gruppe $\mathbb{Z}\times \mathbb{Z}\times \mathbb{Z}/7\mathbb{Z}$ erzeugt. Wir wollen nun überprüfen, ob diese Erzeuger jeweils in den Erzeugnissen obiger Mengen enthalten sind. Dies lässt sich entweder durch ausprobieren tun oder mit dem Gauss-Jordan Algorithmus.

(a) Falsch, wir sehen, dass $(1,0,\overline{0})$ nicht erzeugt wird.
(b) Richtig, setze $v_1=(1,3,\overline{3})$, $v_2=(0,7,\overline{5})$, $v_3=(0,3,\overline{1})$. Dann gilt

$$\begin{array}{rl}(1,0,\overline{0})& =v_1+15v_2-36v_3\\ (0,1,\overline{0})& =-8v_2+19v_3\\ (0,0,\overline{1})& =3v_2-7v_3.\end{array}$$

(c) Richtig, $(1,1,\overline{0})-(1,0,\overline{0})=(0,1,\overline{0})$ und $(0,2,\overline{2})-2\cdot (0,1,\overline{0})=(0,0,\overline{2})$. Da $\mathrm{ggT}(2,7)=1$ erzeugt $\overline{2}$ die Gruppe $\mathbb{Z}/7\mathbb{Z}$. Also erzeugt die Menge $\left\{(1,1,\overline{0}),(0,2,\overline{2}),(1,0,\overline{0})\right\}$ die ganze Gruppe $\mathbb{Z}\times \mathbb{Z}\times \mathbb{Z}/7\mathbb{Z}$.

(a) Richtig
(b) Falsch, man kann zeigen, dass $\phi :S_{100}\to \mathrm{Aut}(S_{100}),\tau \mapsto (\sigma \mapsto \tau \sigma {\tau }^{-1})$ einen Isomorphismus bildet.
(c) Richtig, wir haben letzte Woche gesehen, dass

$$\mathrm{Aut}(\mathbb{Z}/2\mathbb{Z}\times \mathbb{Z}/2\mathbb{Z})\cong {\mathrm{GL}}_2(\mathbb{Z}/2\mathbb{Z}).$$

Man überprüft, dass $|{\mathrm{GL}}_2(\mathbb{Z}/2\mathbb{Z})|=6$. Da ${\mathrm{GL}}_2(\mathbb{Z}/2\mathbb{Z})$ nicht abelsch ist muss es isomorph zu $S_3$ sein. (Es gibt nur zwei Gruppen der Ordnung 6, $S_3$ und $C_6$. Dies lässt sich zum Beispiel mit Cayley-Tabellen beweisen.)

$$\begin{array}{rl}\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)\left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)& =\left(\begin{array}{cc}0& 1\\ 1& 1\end{array}\right)\\ \left(\begin{array}{cc}1& 0\\ 1& 1\end{array}\right)\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)& =\left(\begin{array}{cc}1& 1\\ 1& 0\end{array}\right).\end{array}$$

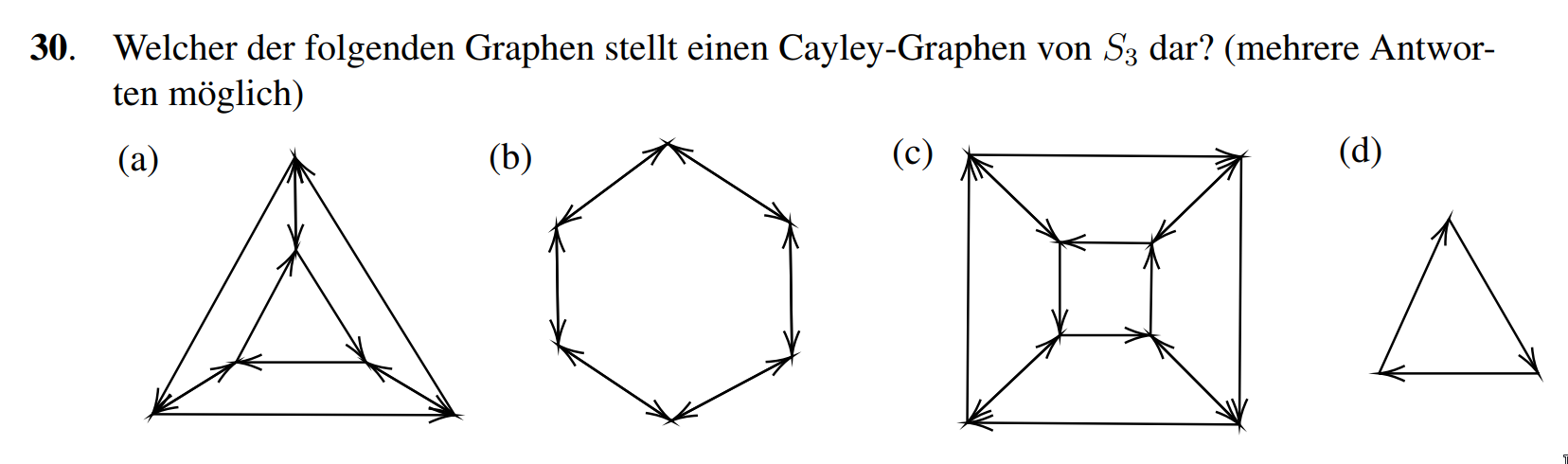
(a) Richtig, mit Erzeuger $r,s$, falls $S_3\cong D_3=⟨r,s\mid r^3=s^2=e\text{ und }srs=r^{-1}⟩$.
(b) Richtig, bemerke, dass $s,rs$ auch $D_3$ erzeugen. Wählt man diese kriegt man obigen Graphen.
(c) Falsch, dies ist der Cayley-Graph von $D_4$. Insbesondere hat dieser acht Elemente.
(d) Falsch, dies ist der Cayley-Graph von $C_3$. Insebsondere hat dieser nur drei Elemente.