Algebra I, MC04

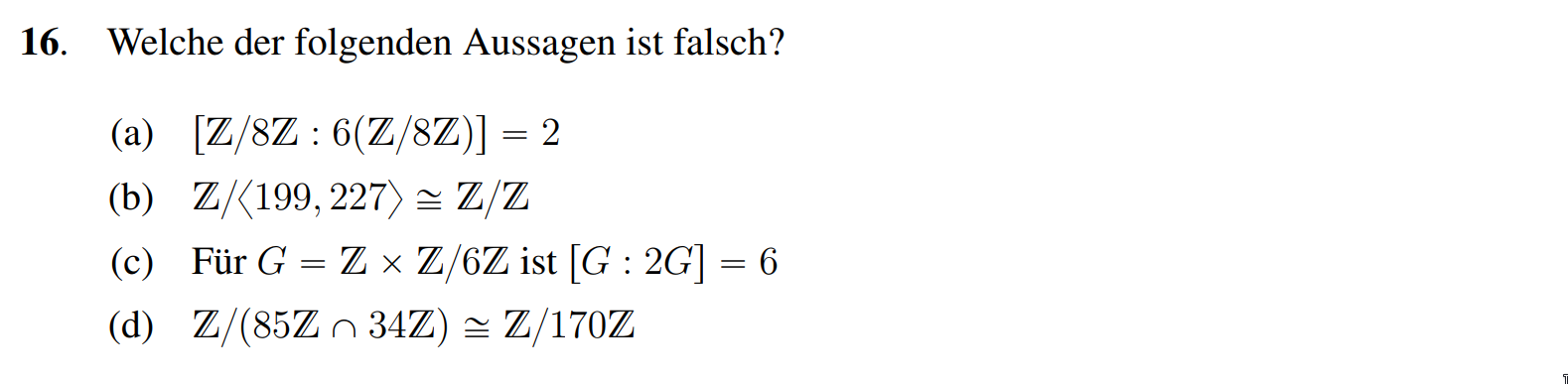
(a) Richtig, eine Rechnung zeigt $6(\mathbb{Z}/8\mathbb{Z})=\left\{[0],[2],[4],[6]\right\}$, also eine Untegruppe der Ordnung $4$. Mit Lagrange folgt $[\mathbb{Z}/8\mathbb{Z}:6(\mathbb{Z}/8\mathbb{Z})]=\frac{|\mathbb{Z}/8\mathbb{Z}|}{|6(\mathbb{Z}/8\mathbb{Z})|}=2$.
(b) Richtig, da $\mathrm{ggt}(199,227)=1$ folgt $⟨199,227⟩=\mathbb{Z}$ (da man mit dem Euklidischen Algorithmus $a,b\in \mathbb{Z}$ erhält, so dass $199a+227b=1$, womit $1\in ⟨199,277⟩$ und somit auch ganz $\mathbb{Z}$). Als Übung führen wir den Algorithmus aus,

$$\begin{array}{rl}227& =1\cdot 199+28\\ 199& =7\cdot 28+3\\ 28& =9\cdot 3+\boxed{1}\\ 3& =3\cdot 1+0.\end{array}$$

Diese Rechnung zeigt, dass der grösste gemeinsame Teiler tatsächlich 1 ist. Des weiteren erhalten wir mit dem üblichen Rechnungsschema

$$\begin{array}{ccccc}& 1& 7& 9& 3\\ 1& 0& 1& -7& 64\\ 0& 1& -1& 8& -73\end{array}$$

also $64\cdot 227-73\cdot 199=1$.
(c) Falsch, wir bemerken, dass $2G=2\mathbb{Z}\times \left\{[0],[2],[4]\right\}\le \mathbb{Z}\times \mathbb{Z}/6\mathbb{Z}$. So gibt es genau vier Nebenklassen. Zum Beispiel mit folgenden Representanten: $(0,[0]),(1,[0]),(0,[1]),(1,[1])$.
(d) Richtig, wir bemerken $85=5\cdot 17$ und $34=2\cdot 17$. Somit gilt $\mathrm{kgV}(34,85)=170$, also $85\mathbb{Z}\cap 34\mathbb{Z}=170\mathbb{Z}$. Dies folgt mit analogem Argument wie in Serie 01 Aufgabe 13, da 170 die kleinste positive Zahl in $85\mathbb{Z}\cap 34\mathbb{Z}$ ist.

(a) Richtig, für alle $n\ge 2$ hat $D_n$ eine Untergruppe isomorph zu $C_n$, diese hat index zwei und ist somit ein Normalteiler. Des weiteren ist $C_n$ abelsch, also ist $D_n$ mit $\left\{e\right\}⊴C_n⊴D_n$ auflösbar.
(b) Richtig, das habt ihr in der Vorlesung gesehen, $\left\{e\right\}⊴C_2\times C_2⊴T⊴C$.A
(c) Falsch, zyklische Gruppen sind immer abelsch und somit auflösbar.
(d) Richtig, $S_3\cong D_3$.

Keine Antwor ist richtig, der Korrekte Stabilisator sollte

$$\left\{\left(\begin{array}{cc}1-2a& a\\ 2-2b& b\end{array}\right)\mid a,b\in \mathbb{Q}\text{ und }b-2a\ne 0\right\}$$

sein.

(b) Falsch, Wir lassen $C_{85}=⟨g⟩$ auf den Ecken von vier verschiedenen 5-Ecken operieren, wobei $g$ einer Rotation um $\frac{2\pi }{5}$ jedes 5-Ecks entspricht. Jedes 5-Eck bildet eine Bahn von 5 Elementen und wir haben keinen Fixpunkt.

(a) Falsch, $(A,(B,M))=ABMBA$, aber $(AB,M)=ABMAB$. Diese sind im allgemeinen nicht gleich, da Matrixmultiplikation nicht kommutativ ist.
(b) Falsch, $(A,(B,M))=A^T{B}^{T}MBA$, aber $(AB,M)=B^T{A}^{T}MAB$. Diese sind wieder im allgemeinen nicht gleich.
(c) Falsch, die Identität in ${\mathrm{GL}}_n(\mathbb{Q})$ ist die Identitätsmatrix $I_n$ mit Einsen auf der Diagonalen. Es gilt aber $I_n+M\ne M$.
(d) Richtig, $(I_n,M)=M{I}_n^T=M$ und $(A,(B,M))=M{B}^T{A}^T=M(AB{)}^T=(AB,M)$.