Algebra I, MC02

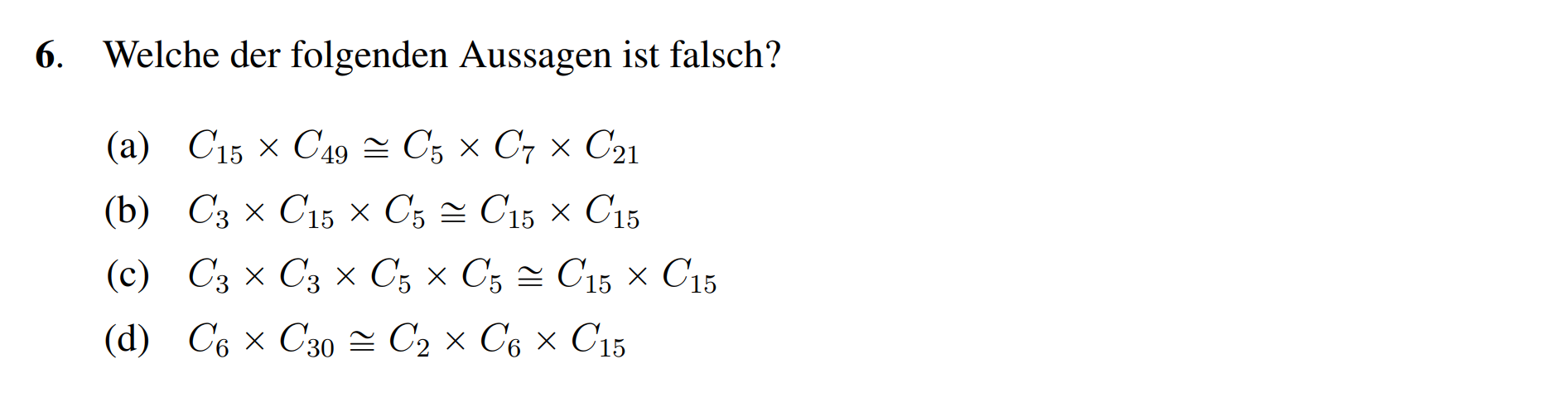
Alles folgt mit Aufgabe 7 aus Serie 01.
(a) Falsch, $C_{49}\ncong C_7\times C_7$
(b) Richtig
(c) Richtig
(d) Richtig

Definiere $D_4=⟨r,s\mid r^4=s^2=e\text{ und }srs=r^{-1}⟩$. Mit dem Satz von Lagrange müssen diese Untergruppen Grad 2 oder 4 haben. Für Grad 2 müssen wir also alle Elemente von Ordnung zwei finden. Wir haben die vier verschiedenen Spiegelungen $s,rs,r^{2}s,r^{3}s$ und die rotation um $\pi$ also $r^2$. Die Elemente $e,r,r^3$ haben alle Ordnung ungleich 2. Wir haben also alle 5 Untergruppen der Ordnung 2 gefunden. Für Untergruppen der Ordnung 4 bemerken wir zuerst, dass $⟨r⟩=⟨r^3⟩=\left\{e,r,r^2,r^3\right\}\cong C_4$ eine solche ist. Zuletzt finden wir durch Betrachten von Erzeugnissen von zwei Elementen $⟨r^2,s⟩=\left\{e,r^2,s,r^{2}s\right\}$ und $⟨r^2,sr⟩=\left\{e,r^2,sr,s{r}^3\right\}$. Man überprüft, dass alle anderen Erzeugnisse von paaren von Elementen die selben oder die ganze Gruppe bilden. Wir kommen also auf insgesamt 8 Untergrupen. Es folgt (a).

(a) Richtig, $\mathrm{ggT}(9,8)=1$
(b) Richtig,
(c) Falsch, $C_4\times C_4\ncong C_{16}$
(d) Richtig, $C_9\times C_7\cong C_{63}$

(a) Falsch, nach Aufgabe 13 alle der Form $n\mathbb{Z}$, unendlich zyklisch.
(b) Falsch, mit Aufgabe 5.
(c) Richtig, $[\mathbb{Z}:n\mathbb{Z}]=n$
(d) Falsch, (a)

Mit obiger Notation gilt $D_6=\left\{e,r,r^2,r^3,r^4,r^5,s,rs,r^{2}s,r^{3}s,r^{4}s,r^{5}s\right\}$. Wir gehen alle Elemente durch und finden, dass folgende Elemente Ordnung 3 haben: $r^2,r^4$. Es folgt (b).